CSS/SVGのtransform matrixを求める。3点からアフィン変換を計算するツール!

あけましておめでとうございます!
2022年最初のブログ記事は、アフィン変換です。
CSSやSVGで図形の位置を変える時に、transformという属性が使えます(transform – CSS: カスケーディングスタイルシート | MDN)。値としては、matrix, rotate, skew, scale といった関数を指定できるものです。これによって、図形や画像を「アフィン変換」で変形・移動ができるという訳です。
その中でも、matrix()という関数は特殊で、他のトランスフォーム関数(回転や縮小拡大)をこれ1つで代用可能なものです。というよりも、matrix()は3×3のアフィン変換行列を指定するための関数で、その特殊な処理をrotate()回転、scale()拡大縮小、のように定義しているに過ぎません。3×3のアフィン変換行列があれば、とりあえず線形変換は全て実行可能、という訳です。
今回は、そんなtransform属性のmatrix()を掘り下げていきます。
matrix()の形式
まずは、CSSやSVGでtransform のmatrix()をどのように記述するのかを見ていきます。
matrix()は、引数として、a b c d e fのように6つの数値を取ります。matrix(a b c d e f)のように指定します。引数の数値の順番が重要です。数式で表すと以下のような行列を指定することになります。
\[ \begin{pmatrix} a & c & e \\ b & d & f \\ 0 & 0 & 1 \\ \end{pmatrix} \]つまり、変換元の座標(src)から、変換先の座標(dest)へのアフィン変換は以下のうように実行されます。
\[ \begin{pmatrix} x_{dest} \\ y_{dest} \\ 1 \\ \end{pmatrix} = \begin{pmatrix} a & c & e \\ b & d & f \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} x_{src} \\ y_{src} \\ 1 \\ \end{pmatrix} \]行列表現で無い場合は、以下のような計算式ですね。
\[ \begin{equation} \begin{aligned} x_{dest}=ax_{src} + cy_{src} + e \\ y_{dest}=bx_{src} + dy_{src} + f \\ \end{aligned} \end{equation} \]角度θ分だけ回転させるようなアフィン変換は以下のようになりますので、CSS/SVGのrotate()関数はアフィン変換行列の特殊ケースだと言えます。
\[ \begin{pmatrix} x_{dest} \\ y_{dest} \\ 1 \\ \end{pmatrix} = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} x_{src} \\ y_{src} \\ 1 \\ \end{pmatrix} \]さて、これらアフィン変換を実際にWebの世界に持ち込みましょう。
CSSの場合、とあるエレメントにこの変換を実行させたい場合は、以下のように書きます。(sample-image-1024.jpgという写真を要素の背景に設定して回転させる場合の例です)
.sample-image-trans {
background-image: url(sample-image-1024.jpg);
width: 1024px;
height: 753px;
transform-origin: top left;
transform: matrix(1.05, -1.00, 0.97, 1.08, -747.88, 430.18);
}SVGの場合、とあるエレメントにこの変換を実行させたい場合は、以下のようにタグの属性としてtransform属性を指定します。
<rect x="10" y="10" width="30" height="20" fill="red"
transform="matrix(1.05, -1.00, 0.97, 1.08, -747.88, 430.18)" />どちらのケースも、要素の左上を原点とし、右がx軸、下がy軸になるようなアフィン変換を適用します。(CSSの場合は、transform-origin属性で左上原点を指定しています)。
で?matrixどうやって求めるの?
CSSやSVGで使い方分かりましたね。
早速、使い込みましょう!
と言いたいところですが…
はて?
この数値は一体どうやって求めるのでしょうか??
実は、アフィン変換行列は、変換先と変換元の座標がそれぞれ3点あると、逆行列の計算により求めることができます。例えば、ある位置に表示されているオブジェクトを、アフィン変換によって「この位置に移動させたい」と思ったとしましょう。「この位置」がという期待値が予めわかっているのであれば、その座標を「変換先」にして元々のオブジェクトの位置「変換元」座標との3点ペアでmatrix()の値が求まる、ということなのです。
アフィン変換は線形変換なので、形がぐにゃっと変わってしまうような変換はできません。そんな変形がたった3点のペアでできるはずがないことは直感的にも判るでしょう。
3点の理屈は、以下の記事が大変参考になります。
3点からアフィン変換行列を求めるオンラインツール
私の場合、ちょいちょいこの計算をやりたかったのでWebベースのツールにしてみました。
OpenCVが使えれば、getAffineTransform()というAPIで同様の行列が得られるようです。私の場合は、ブラウザのツールにしたかったので、逆行列の計算をして求めています。JavaScriptの逆行列の実装は、James D. McCaffreyという先生が作ってくれたものがあったのでそちらを流用させていただいています。
実際に使ってみる
まずは写真を用意します。何でも良かったのですが、iPhoneの写真をpixelsからいただきました。


iPhone Xの写真でしょうか?横向いちゃってますねぇ。
これをちゃんと(?)縦に配置してみましょう。
先程の「3点からアフィン行列を作る」ツールを使います。以下の写真のように、転送元3点を赤丸の座標にします。変換後の座標3点は青丸の位置に取ります。
要は、赤丸の位置にあるiPhoneを青丸の位置に移動させよう、という話です。青丸の位置はここである必要はありません。iPhoneを表示させたい、と思った位置にすればよいのです。


「3点からアフィン行列を作る」ツールのSource points, Destination pointsにそれぞれ3点の座標を入力して、ブルーのボタン「GENERATE AFFINE TRANSFORM」を押します。すると、その下のテキストボックス「Transform value」にCSS/SVGのtransform属性に指定できるそのものの文字列が表示されます。
これが、アフィン変換行列(transformのmatrix()関数の値)です。
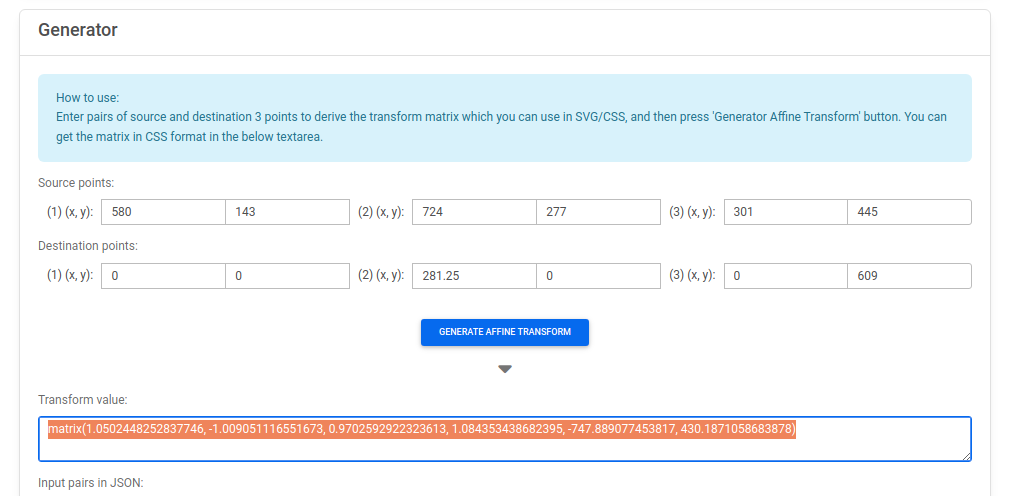

こちらをCSSのtransform属性に指定して実際に横向きだったiPhoneが正しい位置に表示されるか見てみます。
以下の画像をご覧ください。画像サイズがブログのスタイルと違うのでレイアウトが崩れて、ちょっとはみ出ちゃってますが、めでたくiPhoneが縦に表示されています。
下の画像はクリックすると、回転がアニメーションで表示されます。CSSのアニメーションで実現していますのでmatrix()の座標にしがってブラウザが勝手に表示してくれているということです。なんとも有り難い話です。
まとめ
CSS/SVGのtransformのmatrix()について深掘ってみました。
matrix()のパラメータの値を、回転や移動、拡大縮小などシンプルなケースで解説を加えた記事は色々見かけましたが、上記のような用途には使えませんでした。
matrix()の6つのパラメータはどうやって求めるの?という疑問に対して、1つの解が得られたのではないでしょうか。
映画「マトリクス」みるなら、Fire tv で大画面テレビで観よう!






















